Grokking the Coding Interview: Patterns for Coding Questions
See Grokking Pattern 1.
3. Pattern: Fast & Slow pointers
LinkedList Cycle (easy)
题目描述很反人类,但其实就是给你一个链表(只有head指针),让你判断是否有环。进阶是只使用O(1)的空间,也就是常量空间。
有环的链表肯定会访问到重复的节点,环内有1个或以上的节点。搞一个空间存已经访问过的节点,查到之前访问过就能判断了,但空间最坏能到O(n)。常量空间,自然要用快慢指针。
推理一下,快慢指针什么时候能证明链表有环?
猜想肯定是快慢指针指向同一个节点时,但怀疑是否存在“有环链表下快慢指针也不会同时指向同一个节点”。画画图,列一下方程式,假设链表入环前有s个节点,环上有c个节点,可以知道,当走整数倍c(2倍起,同时还得>s)的时候快慢指针是能遇到的,这个值不会不存在,还会多次相遇。所以不用担心快慢节点会永远遇不到。
编码上很简单了,记住init时fast,slow都指向head,然后while内先走再check。
Middle of the LinkedList (easy)
很简单的题,把两个case都手动推理一遍,就知道了。hint:fast先走,提前退出,slow就不用走了。
Start of LinkedList Cycle (medium)
这个题猜得到是需要快慢指针相遇后再加点什么操作的,但是推理容易卡壳。主要还是对快慢指针相遇的情况理解的不够。
快慢指针相遇很好写,node地址相等就是了。但相遇时,快慢指针并不是可能走了无数圈。这里有一个点必须记住,就是“慢指针入环后,和快指针相遇时,慢指针在环上是不会走超过一圈的”。也就是慢指针入环后继续走,一圈以内必定碰到快指针。
这个知识点,我以前应该用方程式推过,也不记得推理有没有漏洞了,这次做题还没推出来。所以这里最直观也正确的解法是数学归纳法。我们讲slow入环后和fast相遇,那么最快相的情况,当然是slow和fast直接在入环点直接相遇,0步。再麻烦点,就是fast在slow的前面(此刻的位置是fast.next==slow),这样两个相邻的节点,只需1步就能相遇。假设fast更远一点,即fast.next.next==slow,就需要2步,以此类推,入环时刻,fast和slow的距离(fast的n个next==slow)假设为n,就需要n步相遇。但fast和slow之间最大距离就是fast在slow的前一个,假设环里有k个节点,fast和slow的最大距离就是k-1,所以最多k-1步,fast和slow必定相遇。所以slow不可能在相遇前走几圈。
知道slow在一圈内就会和fast相遇,其中几个关键长度如下图所示。那么相遇时slow的公式应该写为,slow=a+b,fast=a+b+n(b+c)。
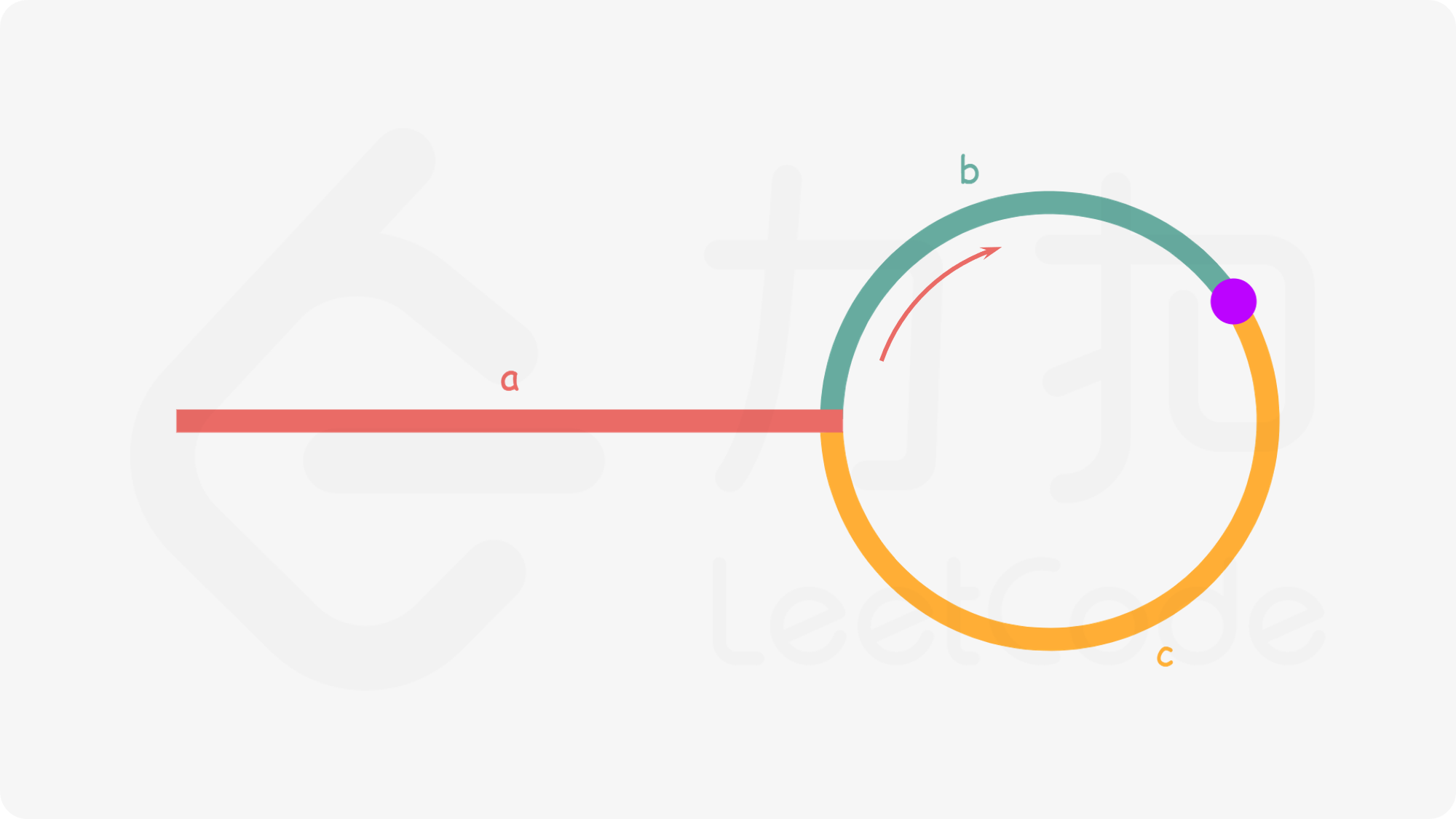
(leetcode图源,可能会挂,自行戳网址)
再回到题目本身,当两指针在紫色点上相遇时,代入化简一下已有式子,得a+b=n(b+c),即a=c+(n-1)(b+c),为什么化简成这样?不是因为这样a可以通过等式右边得到,右边这式子也没法继续求。而是因为,右边写成这样,b+c是一整圈,也就是说,如果一个指针从链表头开始走起,另一个指针从紫色点走了c长度又走了几个完整圈,它们会在入环口相遇,另一个指针走几圈完全不用在意。
但注意,这个式子可能有坑,思考下有没有可能a很小,c很大?
n必然>=1,因为fast肯定走的多点,不然fast=a+b+n(b+c)就不对了。那么,a最小就等于c,不可能比c小。这个事情挺有趣的。没有想到一个很通俗易懂的表达,但数学证明了也就证明了吧。
Happy Number (medium)
这题现在是简单😂
题目没有读仔细,所以第一时间没能察觉到和快慢指针有什么联系。题目表述为“也可能是 无限循环 但始终变不到 1”,我简单地想到了不能一直计算,但忘记了无限循环不是每一次结果都不一样,它只是每次结果都是不是1,不是说每次结果都是从未出现的数字。
接着,就排除了用定义一直计算这种思路,变成了想利用数学之类的其他方法来解决。虽然也推理出了平方和计算中,不能爆出非常大的值,最大32bit的数,十进制也就是13位,就算13位都是9,一次平方和计算下来,也不过1053。而1053的平方和也挺小的,1053以内能算出较大平方和的也就是999。而999再算一步也就是243。
可以明显感觉到,不可能出现一个小的数字经过多次计算膨胀的很大,只可能很大的初始数一下子变得很小。当然像case1中19经过计算会变大,但这都是一定范围,最大不可能超过1053。
然而,从这里开始,我就期待用动态规划一类的方式,类似斐波那契数列,提前算好所有快乐数。所以我认为,可以从1,10,100,1000反推平方和等于它们的数,但是反推的链路有点长,说不定反推也会不能停止,毕竟这个思路不太对劲,可能有不少漏洞。
总结还是应该利用平方和结果范围有限这一点,也就是抽象成链表的有环判定。当然,因为平方和都是即时算的,不像链表问题提前准备好链表。简单的方案就是直接保存之前计算出的结果,也就是不用快慢指针,而是用是否已存在来判断。而如果还是想用快慢指针,可以def一个next函数,考虑到节约空间,next函数只管计算不用缓存。快指针两次next,慢指针一次next就好了。
纯数学的角度其实也可以继续推下去。但需要更仔细的范围研究。所以,回顾之前的推理,最大的数字13个9,也会瞬间收缩到1053,再归纳总结,12个9收缩到。。。4个9收缩到324,这里特别的来了,999到243。为什么说999到243特别,因为这里位数不降了,之前的那些大数都会收缩位数,变得更小,999虽然会经过一次计算变小,但位数不会收。所以一旦计算结果收缩到3位数,接下来的所有平方和结果都是三位数以内,不可能膨胀,且跌入三位数后(三位数后再计算一次),必然困在243以下。而为什么就243了,有没有可能实际数字更小?简单举例99就知道,它能变大到162,也就是涨到三位数,但不可能从三位数继续变大。所以,计算进入243以内后,可能会振荡,比如2位数蹦到3位数,但不可能比243更大,也就是出不去了。
那么,假设计算结果小于等于243时,我们能直接给出结论,是不是快乐数。就不用进入无限的循环了。所以问题变成243以内的数字,哪些是快乐数?
而这样的问题缩减,有什么好处呢?好处在于,243个数字,最大值也就是243,大可以暴力算加是否已存在判定,最大空间复杂度也就到243,比起给一个数就缓存,空间占用要小一些。(其实应该也小不了多少,毕竟收缩很快)但把<=243的数字直接打成表,对于频繁查快乐数的情况,就会节约时间的多。oj时间上节省的会比较明显。如果只是一次快乐数判定,当然打表反而还浪费时间。
Problem Challenge 1 - Palindrome LinkedList (medium)
难度简单。
很明显快慢指针能够找到链表的中部。而中部开始向左向右比对,就能判定是否回文。右半边很顺畅,不用改动,关键在于左半部分。但左半部分再快慢指针途中是被遍历访问过的。这其实也就提示了,如果修改链表,就能降低空间复杂度。题目进阶就是希望用O(1)空间,那大概率就是原地修改链表的左半部分。
很直接的就能想到是反向指。写写画画,不难得到简单的代码。得到了链表中部的指针后,当然是往两边走,逐个对比。但注意,奇数回文串和偶数回文串比较的起点是不一样的。我粗心的只想到了偶数回文,跑测试才发现奇数回文跑不过。
P.S.
这个题还有个递归解法,我不太擅长递归,经常起手就是迭代,所以这里值得再学习下。首先,递归能给我们什么?假设我们只是简单的print val,那么递归就能从尾到头,逆序读出每个节点的值。假设我们递归到底了,现在能读到尾部节点,这个时候我们应该拿头部节点和它进行比较,接着递归会读倒数第二个,而这时又应该拿顺数第二个节点比较。可以看到,从头部开始读也可以用一个指针来解决,但这个指针得是外部的变量,放在递归函数里面太困难了。再思考奇偶情况,奇数节点两指针地址会指向同一个节点,容易判断,偶数情况本来以为会麻烦点,但还好,因为两个指针指向的节点是相邻的,所以只要next判断一下就好了。leetcode官方解更飘逸,全遍历,不用提前返回,那对栈空间要求更高了。不大实用,但可以多熟悉下递归。论简单,还是递归这个写法代码少。
Problem Challenge 2 - Rearrange a LinkedList (medium)
1 | Given the head of a Singly LinkedList, write a method to modify the LinkedList such that the nodes from the second half of the LinkedList are inserted alternately to the nodes from the first half in reverse order. So if the LinkedList has nodes 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> null, your method should return 1 -> 6 -> 2 -> 5 -> 3 -> 4 -> null. |
跟challenge1类似,尝试了一下递归的写法,比较容易写,就是先把偶数链表搞定,再补一下奇数情况的判断就行了。但是注意,debug时别打印链表,修改中途的临时链表很可能是有环的,打印也打不出来。当然可以限制下打印的node个数,调试时还是可以有的。
如果不用递归写法,这个题还是和challenge1一样,可以把后半部分链表原地反转。不多赘述。
Problem Challenge 3 - Cycle in a Circular Array (hard)
题目有点难读,但解析下来,题目的意思是,首先有个环有n个节点,节点里的值表示下一步会向前or向后跳几个节点,可以理解为在做链表的next链接。这样下来很可能会出现环状的链表,而且题目定义的链表更狭窄点,k=1(一个节点自环)的不算,不算一会儿前进一会儿后退的。
根据“链表next”和“判断是否循环”,就知道可以用快慢指针。但快慢指针会测到自环,所以即使判断有环,还得再一次确认是否是k=1自环的情况。
而“不算一会儿前进一会儿后退”这一点很重要,题目的说法是循环的下标序列不是全正就是全负。那么指针跑的时候去要看自己现在所处的位置i,这个位置指定的步数,也就是nums[i]如果和之前的nums[…]符号不同,就可以直接判断为False。
那么,还剩两个问题。
- 快慢指针没有null作为退出条件了,不知道能不能结束。这里可以考虑防御性编程,加个一定限制。但其实不需要,原因是,如果一个nums值全为正,选一个元素来看,它必然得指向某个元素,这个元素如果是它自己,就会发现一个自环;如果不是,它势必要指向一个新元素(我们还未访问的)。但访问得一直继续,如果每次都不是循环(快慢指针查不到的),不会停止,一直访问下去,那么元素迟早被访问完,那下一步会去哪儿呢?所以必然会有快慢指针能够查到的环,虽然自环不能算本题定义的“循环”。
- 总结一下,就是,除了不是全正or全负会提前退出,快慢指针是必然会相遇的。自信点,不用防御编程。
- 此题不是简单的从数组头开始。拿个示例画一下,也能发现,从某个下标开始跑快慢指针,结果都是不一样的。所以理论上,每个数组元素都是可能的循环的开始。
总结到这里,突然想到一个问题,既然只有全正全负会陷入while loop不能提前退出,而全正全负又一定能有广义的环。那么完全不用快慢指针,只需要把每个点当作可能的入环口,也就是从这个点开始我能转回这个点,就找到了一个广义环。并不是非得快慢指针。只是这里有个坑,那就是这个点只是可能的入环口,它也有可能是类似有环链表的直线部分,走了几步才入环。所以得有个限制退出while步进,不然会死循环出不去。又由前面整理的结果,想要全正or全负没有环是不可能的,最大的环也就到整个数组的长度(当然,可能链表箭头走的很骚,不是说只能沿着数组+1/-1步这么走,但长度是不能再长了)。
这个思路比快慢指针代码上简单点,时间复杂度上却不是变少,因为这个思路走满环,最坏时能达到数组长度,O(n),快慢指针中fast指针和slow指针第一次相遇时slow也没有走满环,fast多一倍步数,也没差多少。所以这个思路也不会带来质变,聊胜于无。